Program Slicing (continued)
CSE 662 Fall 2019
September 24
Program Slicing Recap
- Dead Code Elimination
- Highlight Dependent Instructions
- Delta Programs
- Optimization
01: read(N)
02: Z := 0
03: I := 1
04: while (I < N) do
05: read(X)
06: if (X < 0) then
07: Y := f1(X)
else
08: Y := f2(X)
end if
09: Z = f3(Z, Y)
10: I = I + 1
end while
11: write(Z)
Control Flow Graph
Data Flow Dependency
Instruction 4 has a data dependency on 1
01: read(N)
02: Z := 0
03: I := 1
04: while (I < N) do
Data Flow Dependency
Instruction 11 has a data dependency on both 2 and 9
(any unbroken path from write to read counts)
02: Z := 0
...
04: while (I < N) do
...
09: Z = f3(Z, Y)
...
end while
11: write(Z)
Control Flow Dependency
Instruction 8 has a control flow dependency from 6
Instruction 9 has a control flow dependency from 4
04: while (I < N) do
06: if (X < 0) then
else
08: Y := f2(X)
09: Z = f3(Z, Y)
Slicing
Target: Start with a line and a set of variables.
Goal: Find the subset of the program that generates the same values for the specified variables.
Slicing Algorithm
- Assume that the target line reads from the target variables
- Compute the transitive closure of all data dependencies
- Add in control dependencies to any available statement
- Repeat from step 2 until nothing new is added
Function Slices
- Simple: Treat $f(a, b, c)$ as a read/write to/from a, b, c.
- Moderate: Expand out/inline $f(a, b, c)$ then go as normal.
- Up/Down Flow
Up/Down Flow
For call $f(a, b, c)$ with $f$ defined as $\texttt{def } f(x, y, z)$.
define f(x, y, z):
1: x = y + z
2: z = y * z
end
- Add virtual write instructions for each: x, y, z at the start.
- For each variable, compute the slice targetting the variable on the last line of the function. Note down which virtual writes appear in the slice
- Treat each call site as one write for each variable, using the virtual writes to determine which variables the writes depend on.
Worst case assumptions:
- Every variable depends on every other variable
- Every call site depends on every other call sites (external state)
Pointers
1: x = 2
2: y = 3
3: *z = 4
4: write(x)
Does $x$ on the last line depend on line 3?
It depends on what $z$ is
Not just pointers
1: x[0] = 2
2: x[1] = 3
3: x[z] = 4
4: write(x[0])
Does $x[0]$ on the last line depend on line 3?
It also depends on what $z$ is
Which value gets written to can change at runtime.
Idea 1: Worst-case assumptions
- Every variable access depends on all preceeding pointer assignments
- Every pointer reference depends on all preceding assignments
Slightly tighter restrictions possible if referring to an array/struct instead of a pointer
Idea 2: Determine possible program states
Example
struct { int curr; LL *next } LL;
1: read(N)
2: I := 0
3: X := new LL { -1, null }
4: Y := &X->curr
5: while(I < N)
6: X := new LL { I, X }
7: Y := X->next->curr
8: I := I + 1
end while
9: print_ll(X)
What does X depend on as of line 6?
Consider possible state trajectories
- { N = [read value] (line 1) }
- + { I = 0 (line 2) }
- + { X = ptr to $\ell_1$ (line 3); $\ell_1$ = { -1, null } (line 3) }
- + { Y = ptr to $\ell_1$.curr; (line 4) }
- nothing added
- + { X = ptr to $\ell_2$ (line 6); $\ell_2$ = { 0, ptr to $\ell_1$ } (line 6) }
OR nothing added
View each entry in the state trajectory as a set of possible states
| { | N = [read value] (line 1); |
| I = 0 (line 2); | |
| $\ell_1$ = { -1, null } (line 3); | |
| Y = ptr to $\ell_1$.curr; (line 4); | |
| X = ptr to $\ell_2$ (line 6); | |
| $\ell_2$ = { 0, ptr to $\ell_1$ } (line 6) } |
| { | N = [read value] (line 1); |
| I = 0 (line 2); | |
| X = ptr to $\ell_1$ (line 3); | |
| $\ell_1$ = { -1, null } (line 3); | |
| Y = ptr to $\ell_1$.curr; (line 4); } |
| { | N = [read value] (line 1); |
| I = 0 (line 2); | |
| $\ell_1$ = { -1, null } (line 3); | |
| Y = ptr to $\ell_1$.curr; (line 4); | |
| X = ptr to $\ell_2$ OR $\ell_1$ (lines 3 or 6) | |
| $\ell_2$ = { 0, ptr to $\ell_1$ } (line 6) } |
Problem: Infinite possible states!
Each time through the loop we get another $\ell$ assigned.
Observation: Only need to repeat states enough times to get dependencies
Idea: Collapse states into the minimum needed
Collapsing States
- Ignore constants (0, -1, etc...)
- Merge values at unidentified locations (i.e. anything labeled by $\ell$), as long as the dependency data is the same
Simplified Example
struct { int curr; LL *next } LL;
1: read(N)
2: I := 0
3: X := new LL { -1, null }
4: while(I < N)
5: X := new LL { I, X }
6: I := I + 1
end while
7: print_ll(X)
As of Line 4 (0 loops)
| { | N = $\mathbb C$ (line 1); |
| I = $\mathbb C$ (line 2); | |
| $\ell_1$ = { $\mathbb C$, null } (line 3); | |
| X = ptr to $\ell_1$ (line 3) |
As of Line 4 (1 loop)
| { | N = $\mathbb C$ (line 1); |
| I = $\mathbb C$ (line 2); | |
| $\ell_1$ = { $\mathbb C$, null } (line 3); | |
| $\ell_2$ = { $\mathbb C$, ptr to $\ell_1$ } (line 5); | |
| X = ptr to $\ell_2$ (line 5) |
As of Line 4 (2 loops)
| { | N = $\mathbb C$ (line 1); |
| I = $\mathbb C$ (line 2); | |
| $\ell_1$ = { $\mathbb C$, null } (line 3); | |
| $\ell_2$ = { $\mathbb C$, ptr to $\ell_1$ } (line 5); | |
| $\ell_3$ = { $\mathbb C$, ptr to $\ell_2$ } (line 5); | |
| X = ptr to $\ell_2$ (line 5) |
$\ell_2$ and $\ell_3$ are "similar". Replace them with a new virtual $v_4$
As of Line 4 (2+ loops)
| { | N = $\mathbb C$ (line 1); |
| I = $\mathbb C$ (line 2); | |
| $\ell_1$ = { $\mathbb C$, null } (line 3); | |
| $v_4$ = { $\mathbb C$, ptr to $\ell_1$ OR $v_4$ } (line 5); | |
| X = ptr to $v_4$ (line 5) |
Subsumption
State $S_2$ subsumes state $S_1$ if you can reach $S_2$ from $S_1$ by any of...- Add alternatives for pointers
- Add new line dependencies
- Rename an un-identified (i.e., $\ell_i$) location
- Merge values at un-identified (i.e. anything labeled by $\ell$) into a virtual location.
Subsumption
- 0 loops
- 1 loop
- 2+ loops
- 3+ loops
2+ loops subsumes both 1 loop and 3+ loops
Final state representation: { 0 loops; 2+ loops }
Flow Dependencies
- Replay state trajectory.
- Apply virtual node replacements.
- Use computed possible states to determine possible data dependencies.
- Include every possible data dependency.
What if we want to slice a program in the context of specific inputs?
01: read(N)
02: Z := 0
03: I := 1
04: while (I < N) do
05: read(X)
06: if (X < 0) then
07: Y := f1(X)
else
08: Y := f2(X)
end if
09: Z = f3(Z, Y)
10: I = I + 1
end while
11: write(Z)
... with N = 2, X = -4, 3 the trace of this program is
$1^1$ $2^1$ $3^1$ $4^1$ $5^1$ $6^1$ $7^1$ $9^1$ $10^1$ $4^2$ $5^2$ $6^2$ $8^2$ $9^2$ $10^2$ $4^3$ $11^1$
(superscripts distiguish repeated occurrences)
Dynamic Slicing
Instead of considering all paths, focus on the trace under the provided inputs
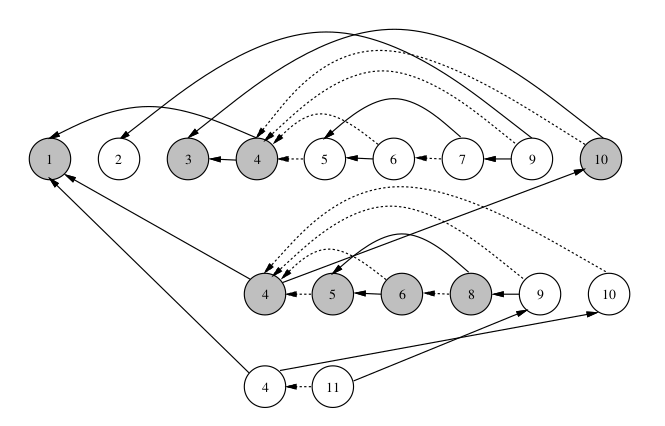
(Dependencies for Y as of $8^2$ on N = 2, X = -4, 3)
- Same as before, but allowed to have multiple copies of nodes.
- Each instruction instance may have different dependencies... only consider the immediately preceding assignemnt to each variable.
- First slice the trace
- Every instruction that appears at least once in the sliced trace is in the final slice
Added benefit: Can handle pointer tracking gracefully: Know exactly what the pointer's value will be.
Bibliography
- Program Slicing (Weiser)
- A Survey of Program Slicing Techniques (Tip)
- Dependence Analysis for Pointer Variables (Horwitz, Pfeiffer, Reps)
- Dynamic Slicing in the Presence of Unconstrained Pointers (Agrawal, DeMillo, Spafford)