CSE-4/562 Spring 2019

Midterm Review

March 11, 2019

What are Databases?

Analysis: Answering user-provided questions about data

What kind of tools can we give end-users?

Declarative Languages
Organizational Datastructures (e.g., Indexes)

Manipulation: Safely persisting and sharing data updates

What kind of tools can we give end-users?

Consistency Primitives
Data Validation Primitives

Primitive: Basic building blocks like Int, Float, Char, String
Tuple: Several ‘fields’ of different types. (N-Tuple = N fields); A Tuple has a ‘schema’ defining each field
Set: A collection of unique records, all of the same type
Bag: An unordered collection of records, all of the same type
List: An ordered collection of records, all of the same type


            SELECT  [DISTINCT] targetlist
            FROM    relationlist
            WHERE   condition

Compute the $2^n$ combinations of tuples in all relations appearing in relationlist
Discard tuples that fail the condition
Delete attributes not in targetlist
If DISTINCT is specified, eliminate duplicate rows

This is the least efficient strategy to compute a query! A good optimizer will find more efficient strategies to compute the same answer.

Physical Layout

Record Formats

Fixed: Constant-size fields. Field $i$ at byte $\sum_{j < i} |Field_j|$
Delimited: Special character or string (e.g., ,) between fields
Header: Fixed-size header points to start of each field

File Formats

Fixed: Constant-size records. Record $i$ at byte $|Record| \times i$
Delimited: Special character or string (e.g., \r\n) at record end
Header: Index in file points to start of each record
Paged: Align records to paging boundaries

File: A collection of pages (or records)
Page: A fixed-size collection of records; Page size is usually dictated by hardware.
Mem Page $\approx$ 4KB Cache Line $\approx$ 64B
Record: One or more fields (for now)
Field: A primitive value (for now)

Relational Algebra

Operation	Sym	Meaning
Selection	$\sigma$	Select a subset of the input rows
Projection	$\pi$	Delete unwanted columns
Cross-product	$\times$	Combine two relations
Set-difference	$-$	Tuples in Rel 1, but not Rel 2
Union	$\cup$	Tuples either in Rel 1 or in Rel 2
Intersection	$\cap$	Tuples in both Rel 1 and Rel 2
Join	$\bowtie$	Pairs of tuples matching a specified condition
Division	$/$	"Inverse" of cross-product
Sort	$\tau_A$	Sort records by attribute(s) $A$
Limit	$\texttt{LIMIT}_N$	Return only the first $N$ records (according to sort order if paired with sort).

Equivalence

$$Q_1 = \pi_{A}\left( \sigma_{c}( R ) \right)$$ $$Q_2 = \sigma_{c}\left( \pi_{A}( R ) \right)$$

$$Q_1 \stackrel{?}{\equiv} Q_2$$

Rule	Notes
$\sigma_{C_1\wedge C_2}(R) \equiv \sigma_{C_1}(\sigma_{C_2}(R))$
$\sigma_{C_1\vee C_2}(R) \equiv \sigma_{C_1}(R) \cup \sigma_{C_2}(R)$	Only true for set, not bag union
$\sigma_C(R \times S) \equiv R \bowtie_C S$
$\sigma_C(R \times S) \equiv \sigma_C(R) \times S$	If $C$ references only $R$'s attributes, also works for joins
$\pi_{A}(\pi_{A \cup B}(R)) \equiv \pi_{A}(R)$
$\sigma_C(\pi_{A}(R)) \equiv \pi_A(\sigma_C(R))$	If $A$ contains all of the attributes referenced by $C$
$\pi_{A\cup B}(R\times S) \equiv \pi_A(R) \times \pi_B(S)$	Where $A$ (resp., $B$) contains attributes in $R$ (resp., $S$)
$R \times (S \times T) \equiv (R \times S) \times T$	Also works for joins
$R \times S \equiv S \times R$	Also works for joins
$R \cup (S \cup T) \equiv (R \cup S) \cup T$	Also works for intersection and bag-union
$R \cup S \equiv S \cup R$	Also works for intersections and bag-union
$\sigma_{C}(R \cup S) \equiv \sigma_{C}(R) \cup \sigma_{C}(S)$	Also works for intersections and bag-union
$\pi_{A}(R \cup S) \equiv \pi_{A}(R) \cup \pi_{A}(S)$	Also works for intersections and bag-union
$\sigma_{C}(\gamma_{A, AGG}(R)) \equiv \gamma_{A, AGG}(\sigma_{C}(R))$	If $A$ contains all of the attributes referenced by $C$

Algorithms

"Volcano" Operators (Iterators): Operators "pull" tuples, one-at-a-time, from their children.
2-Pass (External) Sort: Create sorted runs, then repeatedly merge runs
Join Algorithms: Quickly picking out specific pairs of tuples.
Aggregation Algorithms: In-Memory vs 2-Pass, Normal vs Group-By

Nested-Loop Join

Block-Nested Loop Join

Strategies for Implementing $R \bowtie_{R.A = S.A} S$

Sort/Merge Join: Sort all of the data upfront, then scan over both sides.
In-Memory Index Join (1-pass Hash; Hash Join): Build an in-memory index on one table, scan the other.
Partition Join (2-pass Hash; External Hash Join): Partition both sides so that tuples don't join across partitions.

Sort/Merge Join

Sort/Merge typically expressed as 3 operators
(2xSort + Merge)

1-Pass Hash Join

2-Pass Hash Join

Limited Queries: Only supports join conditions of the form $R.A = S.B$
Low Memory: Never need more than 1 pair of partitions in memory
High IO Cost: Every record gets written out to disk, and back in.

Can partition on data-values to support other types of queries.

Index Nested Loop Join

To compute $R \bowtie_{R.A < S.B} S$ with an index on $S.B$

Read One Row of $R$
Get the value of $R.A$
Start index scan on $S.B > [R.A]$
Return rows as normal

Basic Aggregate Pattern

Init: Define a starting value for the accumulator
Fold(Accum, New): Merge a new value into the accumulator
Finalize(Accum): Extract the aggregate from the accumulator.

Basic Aggregate Types

Grey et. al. "Data Cube: A Relational Aggregation Operator Generalizing Group-By, Cross-Tab, and Sub-Totals

Distributive: Finite-sized accumulator and doesn't need a finalize (COUNT, SUM)
Algebraic: Finite-sized accumulator but needs a finalize (AVG)
Holistic: Unbounded accumulator (MEDIAN)

Grouping Algorithms

2-pass Hash Aggregate: Like 2-pass Hash Join: Distribute groups across buckets, then do an in-memory aggregate for each bucket.
Sort-Aggregate: Like Sort-Merge Join: Sort data by groups, then group elements will be adjacent.

Indexing

Data Organization

Unordered Heap: No organization at all. $O(N)$ reads.
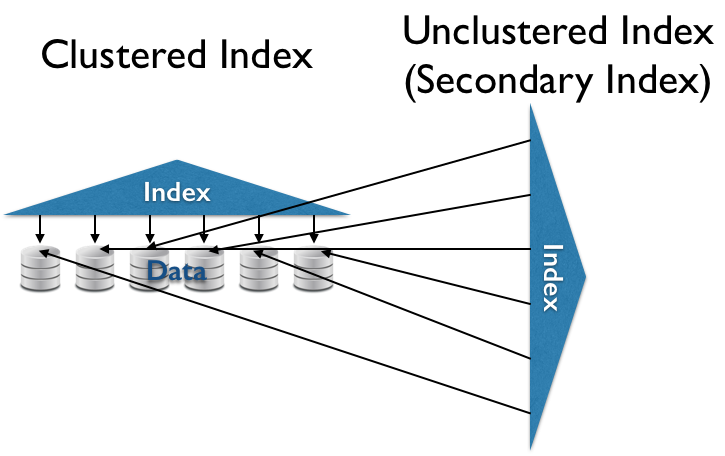
(Secondary) Index: Index structure over unorganized data. $O(\ll N)$ random reads for some queries.
Clustered (Primary) Index: Index structure over clustered data. $O(\ll N)$ sequential reads for some queries.

Data Organization

Tree-Based Indexes

Rules of B+Trees

Keep space open for insertions in inner/data nodes.: ‘Split’ nodes when they’re full
Avoid under-using space: ‘Merge’ nodes when they’re under-filled

Maintain Invariant: All Nodes ≥ 50% Full

(Exception: The Root)

Problems

$N$ is too small: Too many overflow pages (slower reads).
$N$ is too big: Too many normal pages (wasted space).

Problems

Changing hash functions reallocates everything: Only double/halve the size of a hash function
Changing sizes still requires reading everything: Idea: Only redistribute buckets that are too big

Cost-Based Optimization

Accounting

Figure out the cost of each individual operator.

Only count the number of IOs added by each operator.

Operation	RA	IOs Added (#pages)	Memory (#tuples)
Table Scan	$R$	$\frac{\|R\|}{\mathcal P}$	$O(1)$
Projection	$\pi(R)$	$0$	$O(1)$
Selection	$\sigma(R)$	$0$	$O(1)$
Union	$R \uplus S$	$0$	$O(1)$
Sort (In-Mem)	$\tau(R)$	$0$	$O(\|R\|)$
Sort (On-Disk)	$\tau(R)$	$\frac{2 \cdot \lfloor log_{\mathcal B}(\|R\|) \rfloor}{\mathcal P}$	$O(\mathcal B)$
(B+Tree) Index Scan	$Index(R, c)$	$\log_{\mathcal I}(\|R\|) + \frac{\|\sigma_c(R)\|}{\mathcal P}$	$O(1)$
(Hash) Index Scan	$Index(R, c)$	$1$	$O(1)$

Tuples per Page ($\mathcal P$) – Normally defined per-schema
Size of $R$ ($|R|$)
Pages of Buffer ($\mathcal B$)
Keys per Index Page ($\mathcal I$)

Operation	RA	IOs Added (#pages)	Memory (#tuples)
Nested Loop Join (Buffer $S$ in mem)	$R \times S$	$0$	$O(\|S\|)$
Nested Loop Join (Buffer $S$ on disk)	$R \times_{disk} S$	$(1+ \|R\|) \cdot \frac{\|S\|}{\mathcal P}$	$O(1)$
1-Pass Hash Join	$R \bowtie_{1PH, c} S$	$0$	$O(\|S\|)$
2-Pass Hash Join	$R \bowtie_{2PH, c} S$	$\frac{2\|R\| + 2\|S\|}{\mathcal P}$	$O(1)$
Sort-Merge Join	$R \bowtie_{SM, c} S$	[Sort]	[Sort]
(Tree) Index NLJ	$R \bowtie_{INL, c}$	$\|R\| \cdot (\log_{\mathcal I}(\|S\|) + \frac{\|\sigma_c(S)\|}{\mathcal P})$	$O(1)$
(Hash) Index NLJ	$R \bowtie_{INL, c}$	$\|R\| \cdot 1$	$O(1)$
(In-Mem) Aggregate	$\gamma_A(R)$	$0$	$adom(A)$
(Sort/Merge) Aggregate	$\gamma_A(R)$	[Sort]	[Sort]

Tuples per Page ($\mathcal P$) – Normally defined per-schema
Size of $R$ ($|R|$)
Pages of Buffer ($\mathcal B$)
Keys per Index Page ($\mathcal I$)
Number of distinct values of $A$ ($adom(A)$)

Estimating IOs requires Estimating $|Q(R)|$

Operator	RA	Estimated Size
Table	$R$	$\|R\|$
Projection	$\pi(Q)$	$\|Q\|$
Union	$Q_1 \uplus Q_2$	$\|Q_1\| + \|Q_2\|$
Cross Product	$Q_1 \times Q_2$	$\|Q_1\| \times \|Q_2\|$
Sort	$\tau(Q)$	$\|Q\|$
Limit	$\texttt{LIMIT}_N(Q)$	$N$
Selection	$\sigma_c(Q)$	$\|Q\| \times \texttt{SEL}(c, Q)$
Join	$Q_1 \bowtie_c Q_2$	$\|Q_1\| \times \|Q_2\| \times \texttt{SEL}(c, Q_1\times Q_2)$
Distinct	$\delta_A(Q)$	$\texttt{UNIQ}(A, Q)$
Aggregate	$\gamma_{A, B \leftarrow \Sigma}(Q)$	$\texttt{UNIQ}(A, Q)$

$\texttt{SEL}(c, Q)$: Selectivity of $c$ on $Q$, or $\frac{|\sigma_c(Q)|}{|Q|}$
$\texttt{UNIQ}(A, Q)$: # of distinct values of $A$ in $Q$.

(Some) Estimation Techniques

Guess Randomly: Rules of thumb if you have no other options...
Uniform Prior: Use basic statistics to make a very rough guess.
Sampling / History: Small, Quick Sampling Runs (or prior executions of the query).
Histograms: Using more detailed statistics for improved guesses.
Constraints: Using rules about the data for improved guesses.

Sketching

Flips	Score	Probability	E[# Games]
(👽)	0	0.5	2
(🐕)(👽)	1	0.25	4
(🐕)(🐕)(👽)	2	0.125	8
(🐕)$\times N$ (👽)	$N$	$\frac{1}{2^{N+1}}$	$2^{N+1}$

If I told you that in a series of games, my best score was $N$, you might expect that I played $2^{N+1}$ games.

To do that, I only need to track my top score!

Flajolet-Martin Sketches

($\approx$ HyperLogLog)

For each record...
1. Hash each record
2. Find the index of the lowest-order non-zero bit
3. Add the index of the bit to a set
Find $R$, the lowest index not in the set
Estimate Count-Distinct as $\frac{2^R}{\phi}$ ($\phi \approx 0.77351$)
Repeat (in parallel) as needed

Count Sketches

Pick a number of "trials" and a number of "bins"
For each record $O_i$
1. For each "trial" $j$
  1. Use a hash function $h_j(O_i)$ to pick a bin
  2. Add a $\pm 1$ value determined by hash function $\delta_j(O_i)$ to the bin

For each trial $j$, estimate the count of $O_i$ by the value of bin $h_j(O_i)$

Take the median value for all trials.

Count-Min Sketches

Pick a number of "trials" and a number of "bins"
For each record $O_i$
1. For each "trial" $j$
  1. Use a hash function $h_j(O_i)$ to pick a bin
  2. Add 1 to the bin

For each trial $j$, estimate the count of $O_i$ by the value of bin $h_j(O_i)$

Take the minimum value for all trials.

Flajolet-Martin Sketches (HyperLogLog): Estimating Count-Distinct
Count Sketches: Estimating Count-GroupBy
(roughly uniform counts)
Count-Min Sketches: Estimating Count-GroupBy
(small number of heavy hitters)

The `WINDOW` Operator

Define a Sequence (i.e., sort the relation)
Compute all subsequences
- Fixed Physical Size: N records exactly.
- Fixed Logical Size: Records within N units of time.
Compute an aggregate for each subsequence (one output row per subsequence)


    SELECT L.state, T.month, 
       AVG(S.sales) OVER W as movavg
    FROM   Sales S, Times T, Locations L
    WHERE  S.timeid = T.timeid 
      AND  S.locid = L.locid
    WINDOW W AS ( 
       PARTITION BY L.state
       ORDER BY T.month
       RANGE BETWEEN INTERVAL ‘1’ MONTH PRECEDING
             AND INTERVAL ‘1’ MONTH FOLLOWING
    )

Summary

Push vs Pull Data Flow: Push is a better fit because sources produce data at different rates.
Revisit Joins: Focus on ripple-style WINDOW joins.
Revisit Indexing: Linked Hash/Tree Indexes for efficient windowed indexing.
Revisit Aggregation: Sliding window aggregates.

Midterm Review

CSE-4/562 Spring 2019

Physical Layout

Record Formats

File Formats

Relational Algebra

Equivalence

Algorithms

Nested-Loop Join

Block-Nested Loop Join

Strategies for Implementing $R \bowtie_{R.A = S.A} S$

Sort/Merge Join

Sort/Merge Join

Sort/Merge Join

1-Pass Hash Join

2-Pass Hash Join

Index Nested Loop Join

Basic Aggregate Pattern

Basic Aggregate Types

Grouping Algorithms

Data Organization

Data Organization

Data Organization

Tree-Based Indexes

Rules of B+Trees

Problems

Problems

Accounting

(Some) Estimation Techniques

Sketching

Flajolet-Martin Sketches

($\approx$ HyperLogLog)

Count Sketches

Count-Min Sketches

The WINDOW Operator

Summary

The `WINDOW` Operator