CSE-250 Fall 2022 - Section B

Graphs

CSE-250 Fall 2022 - Section B

Oct 5, 2022

Textbook: Ch. 15.3

Graphs

A graph is a pair $(V, E)$ where

$V$ is a set of vertices
$E$ is a set of vertex pairs called edges
edges and vertices may also store data (labels)

Graphs

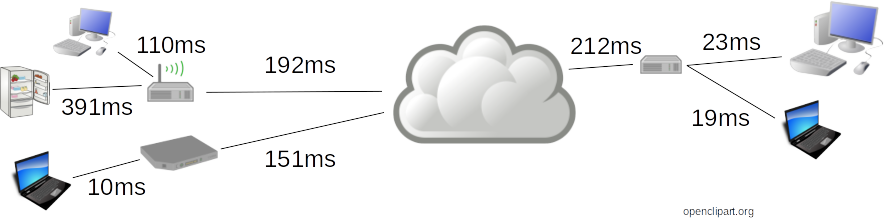
Example: A computer network
(edges store ping, nodes store addresses)

Edge Types

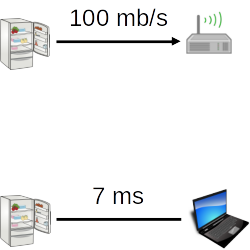
Directed Edge (e.g., transmit bandwidth)

Ordered pair of vertices $(u, v)$
origin ($u$) → destination ($v$)

Undirected edge (e.g., round-trip latency)

Unordered pair of vertices $(u, v)$

Directed Graph

All edges are directed

Undirected Graph

All edges are undirected

Other Applications

Transportation (Flight/Road/Rail Routing)
Protein/Protein Interactions
Social Networks
Dependency Tracking (e.g., make)
Taxonomies

Terminology

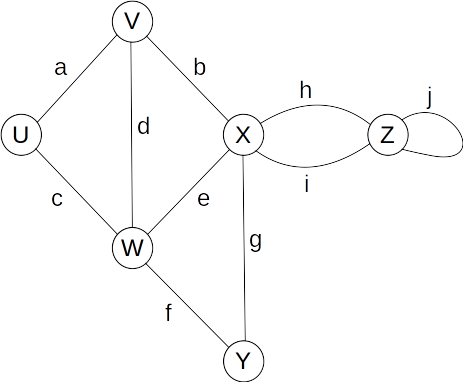
Endpoints (end-vertices) of an edge: U, V are the endpoints of a
Edges incident on a vertex: a, b, d are incident on V
Adjacent Vertices: U, V are adjacent
Degree of a vertex (# of incident edges): X has degree 5
Parallel Edges: h, i are parallel
Self-Loop: j is a self-loop
Simple Graph: A graph without parallel edges or self-loops

Terminology

Path: Sequence of alternating vertices and edges; begins with a vertex; ends with a vertex; each edge is preceded and followed by its endpoints
Simple Path: path such that all of its vertices and edges are distinct
Examples

Terminology

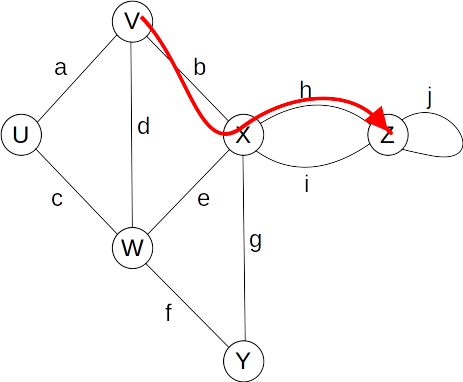
Path: Sequence of alternating vertices and edges; begins with a vertex; ends with a vertex; each edge is preceded and followed by its endpoints
Simple Path: path such that all of its vertices and edges are distinct
Examples: V, b, X, h, Z is a simple path.

Terminology

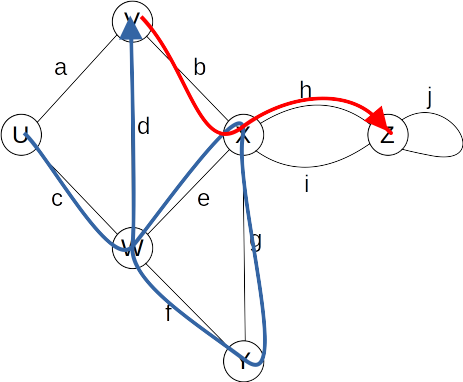
Path: Sequence of alternating vertices and edges; Begins with a vertex; Ends with a vertex; Each edge is preceded and followed by its endpoints
Simple Path: Path such that all of its vertices and edges are distinct
Examples: V, b, X, h, Z is a simple path.; U, c, W, e, X, g, Y, f, W, d, V is a path that is not simple.

Terminology

Cycle: Path that begins and ends with the same vertex; Must contain at least one edge
Simple Cycle: Cycle such that all of its vertices and edges are distinct
Examples

Terminology

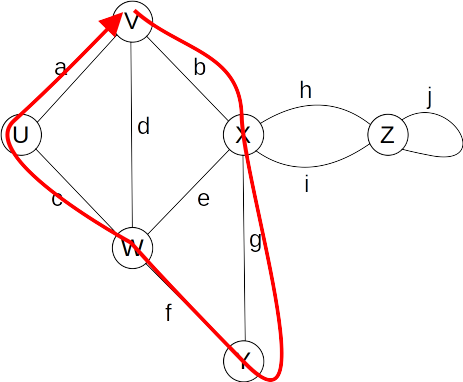
Cycle: Path that begins and ends with the same vertex; Must contain at least one edge
Simple Cycle: Cycle such that all of its vertices and edges are distinct
Examples: V, b, X, g, Y, f, W, c, U, a, V is a simple cycle

Terminology

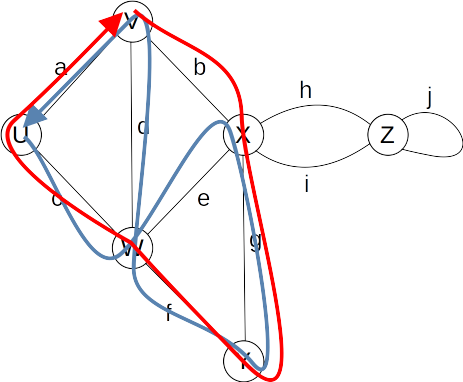
Cycle: Path that begins and ends with the same vertex; Must contain at least one edge
Simple Cycle: Cycle such that all of its vertices and edges are distinct
Examples: V, b, X, g, Y, f, W, c, U, a, V is a simple cycle; U, c, W, e, X, g, Y, f, W, d, V is a cycle that is not simple

Notation

$n$: The number of vertices
$m$: The number of edges
$deg(v)$: The degree of vertex $v$

Graph Properties

$$\sum_{v} deg(v) = 2m$$

Proof: Each edge is counted twice

Graph Properties

In a directed graph with no self-loops and no parallel edges:

$$m \leq n(n-1)$$

No parallel edges: each pair connected at most once
No self loops: pick each vertex once

$n$ choices for the first vertex; $(n-1)$ choices for the second vertex. $$m \leq n(n-1)$$

Hey, isn't this a data structures class?

A (Directed) Graph ADT

Two type parameters (Graph[V, E]): V: The vertex label type; E: The edge label type
Vertices: ... are elements (like Linked List Nodes); ... store a value of type V
Edges: ... are elements; ... store a value of type E

A (Directed) Graph ADT


  trait Graph[V, E] {
    def vertices: Iterator[Vertex]
    def edges: Iterator[Edge]
    def addVertex(label: V): Vertex
    def addEdge(orig: Vertex, dest: Vertex, label: E): Edge
    def removeVertex(vertex: Vertex): Unit
    def removeEdge(edge: Edge): Unit
  }

A (Directed) Graph ADT


  trait Vertex[V, E] {
    def outEdges: Seq[Edge]
    def inEdges: Seq[Edge]
    def incidentEdges: Iterator[Edge] = outEdges ++ inEdges
    def edgeTo(v: Vertex): Boolean
    def label: V
  }

  trait Edge[V, E] {
    def origin: Vertex
    def destination: Vertex
    def label: E
  }

Attempt 1: Edge List

Data Model

A List of Edges: ArrayBuffer
A List of Vertices: ArrayBuffer

Attempt 1: Edge List


    class DirectedGraphV1[V, E] extends Graph[V, E]
    {
      val vertices = mutable.Buffer[Vertex]()
      val edges    = mutable.Buffer[Edge]()

      /* ... */
    }

Attempt 1: Edge List


    def addVertex(label: V): Vertex =
      vertices.append(new Vertex(label))

What's the complexity?

Attempt 1: Edge List


    def addEdge(orig: Vertex, dest: Vertex, label: E): Edge =
      edges.append(new Edge(orig, dest, label))

What's the complexity?

Attempt 1: Edge List


    def removeEdge(edge: Edge): Unit =
      edges.subtractOne(edge)

What's the complexity? ($O(n)$)

Attempt 2: Linked Edge List

Data Model

A List of Edges: DoublyLinkedList
A List of Vertices: DoublyLinkedList

DoublyLinkedList


  class DoublyLinkedList[T] extends Seq[T] {
    def append(element: T): Node =
      /* O(1) with tail pointer */

    def remove(node: Node): Unit =
      /* O(1) */

    def iterator: Iterator[T]: Unit =
      /* O(1) + O(1) per call to next */
  }

Attempt 2: Linked Edge List


    class DirectedGraphV2[V, E] extends Graph[V, E] {
      val vertices = DoublyLinkedList[Vertex]()

      class Vertex(label: V) = {
        var node: DoublyLinkedList[Vertex].Node = null
        /* ... */
      }

      def addVertex(label: V): Vertex = {
        val vertex = new Vertex(label)
        val node = vertices.append(vertex)
        vertex.node = node
        return vertex
      }
      /* ... */
    }

What's the complexity?

Attempt 2: Linked Edge List


    class DirectedGraphV2[V, E] extends Graph[V, E] {
      val edges = DoublyLinkedList[Edge]()

      class Edge(orig: Vertex, dest: Vertex, label: E) = {
        var node: DoublyLinkedList[Edge].Node = null
        /* ... */
      }

      def addEdge(orig: Vertex, dest: Vertex, label: E): Vertex = {
        val edge = new Edge(orig, dest, label)
        val node = edges.append(vertex)
        edge.node = node
        return edge
      }
      /* ... */
    }

What's the complexity?

Attempt 2: Linked Edge List


    class DirectedGraphV2[V, E] extends Graph[V, E] {
      val edges = DoublyLinkedList[Edge]()

      def removeEdge(edge: Edge): Unit = {
        edges.remove(edge.node)
      }
      /* ... */
    }

What's the complexity?

Attempt 2: Linked Edge List


    class DirectedGraphV2[V, E] extends Graph[V, E] {
      val vertices = DoublyLinkedList[Vertex]()

      def removeVertex(vertex: Vertex): Unit = {
        vertices.remove(vertex.node)
      }
      /* ... */
    }

What if there's an edge to/from vertex?

Attempt 2: Linked Edge List


    class DirectedGraphV2[V, E] extends Graph[V, E] {
      val vertices = DoublyLinkedList[Vertex]()

      def removeVertex(vertex: Vertex): Unit = {
        vertices.remove(vertex.node)
        for(edge <- vertex.incidentEdges){
          removeEdge(edge)
        }
      }
      /* ... */
    }

What's the complexity? ($O(1) + O(T_{incidentEdges}(n, m))$)

Attempt 2: Linked Edge List


    class DirectedGraphV2[V, E] extends Graph[V, E] {
      val vertices = DoublyLinkedList[Vertex]()
      val edges = DoublyLinkedList[Edge]()

      class Vertex(label: V) = {
        /* ... */

        def outEdges = 
          vertices.filter { _.orig = this }

        def inEdges = 
          vertices.filter { _.dest = this }
      }
      /* ... */
    }

What's the complexity? ($O(m) = O(n^2)$)

Edge List

Edge List Summary

addEdge, addVertex: $O(1)$
removeEdge: $O(1)$
removeVertex: $O(m)$
vertex.incidentEdges: $O(m)$
vertex.edgeTo: $O(m)$
Space Used: $O(n) + O(m)$

Idea: Store the in/out edges for each vertex.

Attempt 3: Adjacency List


    class DirectedGraphV3[V, E] extends Graph[V, E] {
      val vertices = DoublyLinkedList[Vertex]()

      class Vertex(label: V) = {
        var node: DoublyLinkedList[Vertex].Node = null
        val inEdges = DoublyLinkedList[Edge]()
        val outEdges = DoublyLinkedList[Edge]()
        /* ... */
      }
      /* ... */
    }

Attempt 3: Adjacency List


    class DirectedGraphV3[V, E] extends Graph[V, E] {
      /* ... */
      def addEdge(orig: Vertex, dest: Vertex, label: E): Vertex = {
        val edge = new Edge(orig, dest, label)
        val node = edges.append(vertex)
        edge.node = node
        orig.outEdges.append(edge)
        dest.inEdges.append(edge)
        return edge
      }
      /* ... */
    }

What's the complexity?

Attempt 3: Adjacency List


    class DirectedGraphV3[V, E] extends Graph[V, E] {
      /* ... */
      def removeEdge(edge: Edge): Unit = {
        edges.remove(edge.node)
        edge.orig.outEdges.subtractOne(edge)
        edge.dest.inEdges.subtractOne(edge)
      }
      /* ... */
    }

What's the complexity?

Attempt 4: Adjacency List


    class DirectedGraphV4[V, E] extends Graph[V, E] {
      /* ... */
      class Edge(orig: Vertex, dest: Vertex, label: E) = {
        var node: DoublyLinkedList[Edge].Node = null
        var origNode: DoublyLinkedList[Edge].Node = null
        var destNode: DoublyLinkedList[Edge].Node = null
        /* ... */
      }
      /* ... */
    }

Attempt 4: Adjacency List


    class DirectedGraphV4[V, E] extends Graph[V, E] {
      /* ... */
      def addEdge(orig: Vertex, dest: Vertex, label: E): Vertex = {
        val edge = new Edge(orig, dest, label)
        val node = edges.append(vertex)
        edge.node = node
        edge.origNode = orig.outEdges.append(edge)
        edge.destNode = dest.inEdges.append(edge)
        return edge
      }
      /* ... */
    }

What's the complexity?

Attempt 4: Adjacency List


    class DirectedGraphV4[V, E] extends Graph[V, E] {
      /* ... */
      def removeEdge(edge: Edge): Unit = {
        edges.remove(edge.node)
        edge.orig.outEdges.remove(edge.origNode)
        edge.dest.inEdges.remove(edge.destNode)
      }
      /* ... */
    }

What's the complexity?

Attempt 4: Adjacency List


    class DirectedGraphV4[V, E] extends Graph[V, E] {
      /* ... */
      def removeVertex(vertex: Vertex): Unit = {
        vertices.remove(vertex.node)
        for(edge <- vertex.incidentEdges){
          removeEdge(edge)
        }
      }
      /* ... */
    }

What's the complexity?

Adjacency List Summary

addEdge, addVertex: $O(1)$
removeEdge: $O(1)$
vertex.incidentEdges: $O(deg(vertex))$
removeVertex: $O(deg(vertex))$
vertex.edgeTo: $O(deg(vertex))$
Space Used: $O(n) + O(m)$

Adjacency Matrix

Adjacency Matrix Summary

addEdge, removeEdge: $O(1)$
addVertex, removeVertex: $O(n^2)$
vertex.incidentEdges: $O(n)$
vertex.edgeTo: $O(1)$
Space Used: $O(n^2)$