Overlay Spreadsheets

Oliver Kennedy

University at Buffalo

Boris Glavic

Illinois Institute of Technology

Michael Brachmann

Breadcrumb Analytics

The Vizier Notebook

1. Vizier is a Workflow System

2. Vizier isn't Just Code

Including...

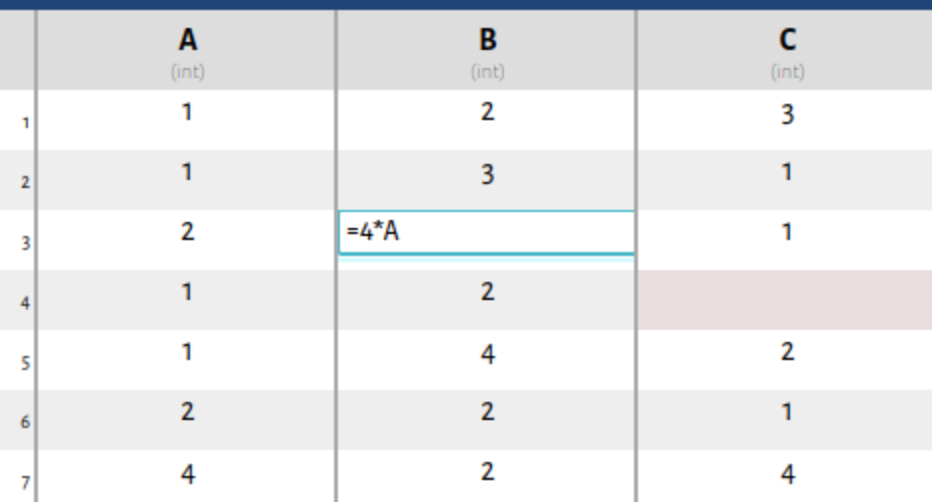
Spreadsheets in Workflows

(Wrangler: Interactive Visual Specification of Data Transformation Scripts; Kandel et al; CHI 2011)

Spreadsheets in Workflows

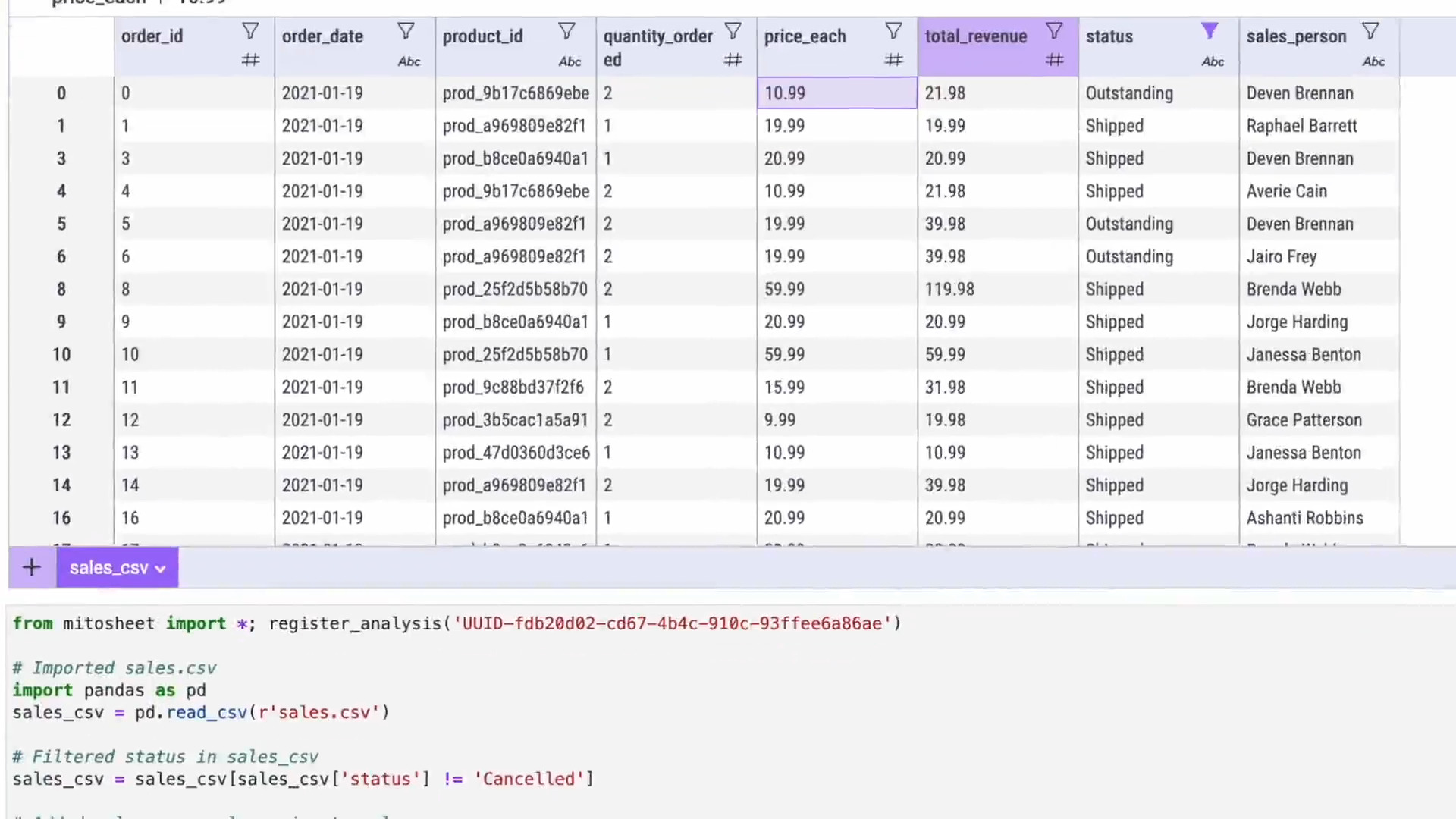(trymito.io)

“Spreadsheets" in Workflows

(The Exception that Improves the Rule; Freire et. al.; HILDA 2016)

Spreadsheets as Workflow Precursors

So why not just use a spreadsheet?

Goals

Build a spreadsheet...
... that can replay edits on a new dataset.
... while supporting "free-form" editing.

So we built a spreadsheet...

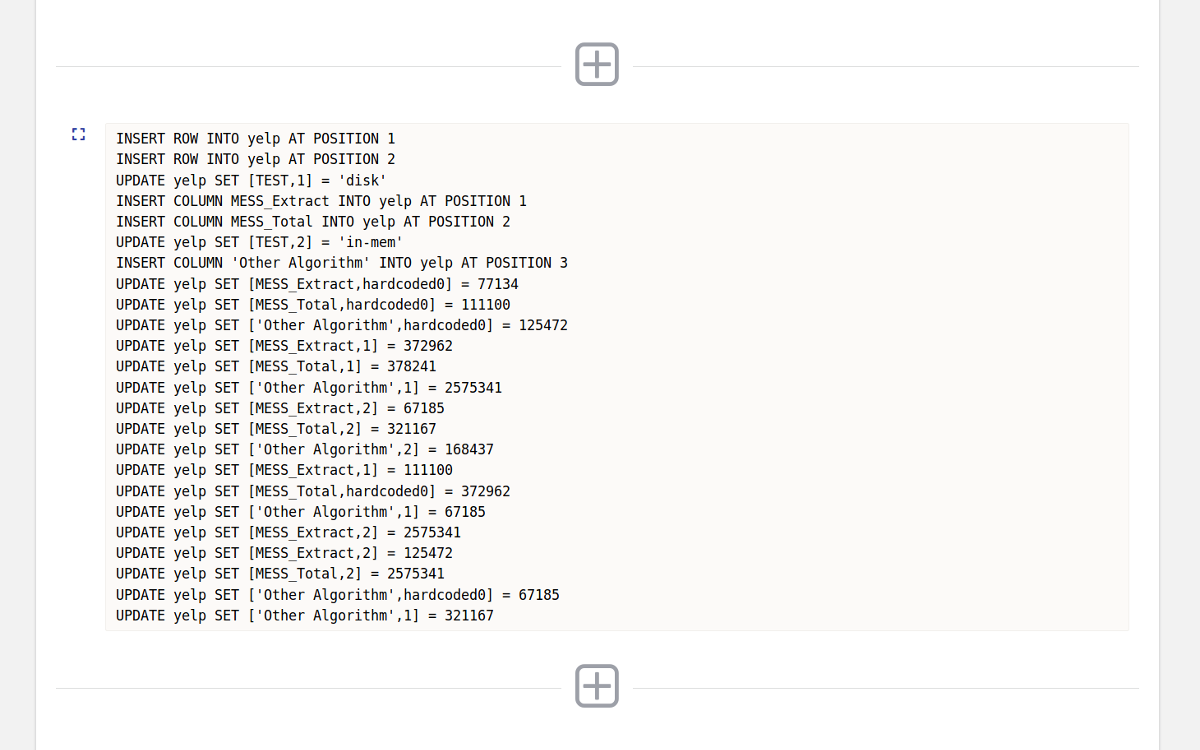
Replaying Shape Updates
Replaying Content Updates

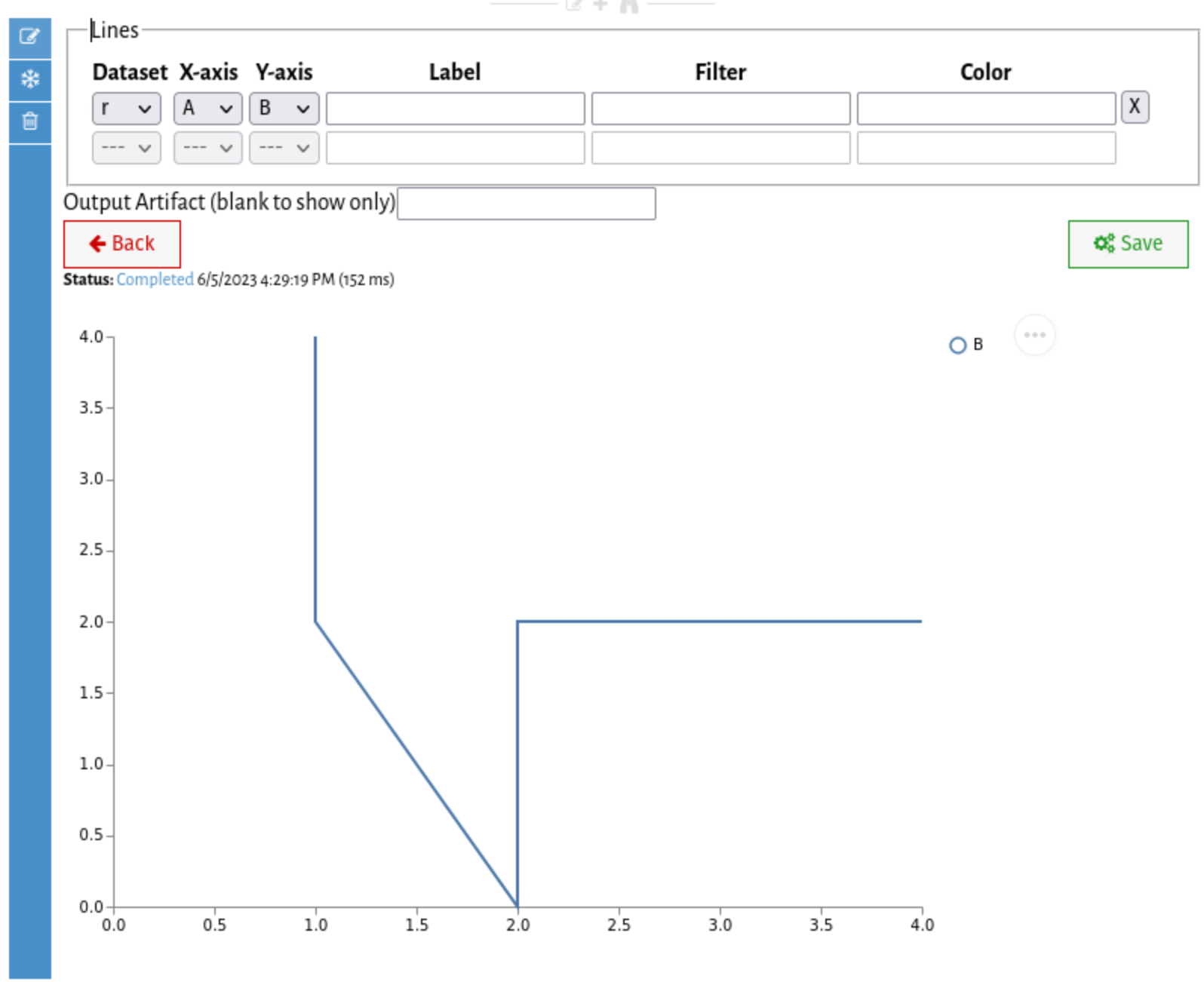
Shape Changes

Mapping Functions

$row(n) = \begin{cases} n & \textbf{if } \color{#d40000}{\blacksquare}, \color{#6c5353}{\blacksquare}\\ n+1 & \textbf{if } \color{#008080}{\blacksquare}, \color{#a05a2c}{\blacksquare}\\ n-3 & \textbf{if } \color{#808000}{\blacksquare} \end{cases}$ $col(n) = \begin{cases} n & \textbf{if } \color{#d40000}{\blacksquare}, \color{#008080}{\blacksquare}\\ n-1 & \textbf{if } \color{#6c5353}{\blacksquare}, \color{#a05a2c}{\blacksquare}\\ \texttt{null} & \textbf{if } \color{#536c53}{\blacksquare}\\ \end{cases}$

Content Updates

Coping with Big Data

Classical Spreadsheets (Excel, Google Sheets, etc...)
DataSpread (Bendre et. al.; ICDE 2018)
Ignore the Problem (This Talk)

Patterns

Coping with Big Data

Only materialize the subset of visible rows
(and/or columns)

Restricting the Source Data

Restricting the Overlay

We need to materialize the
transitive closure
of the cell dependencies.

Restricting the Overlay

Spreadsheets are optimized for reactive, interactive computation over cells.

... but here we have a big bulk computation.

Recursive Patterns

$$H[0] = G[0]$$ $$H[n] = G[n] + H[n-1]$$

↓ $$H[n] = sum(G[0:n])$$

Many common patterns have an
equivalent closed-form representation.

Recursive Patterns

$$H[0:1] = G[0:1]$$ $$H[n] = G[n] + H[n-2]$$

↓


  SELECT G + lag(H, 2) AS H OVER (ORDER BY row) FROM ...

Window queries work for the rest.

Recursive Patterns

https://vizierdb.info

Decoupling edits from source data enables spreadsheets in workflow systems
Overlays support a (fast) hybrid batch/reactive execution model.

Open Challenges

Freeform edits don't usually map nicely to structured dataframes.
Content updates don't generalize through external changes in shape.
[Your challenge/comment here]