Indexes

Recap

Data, even if well organized still requires you to page through a lot.

An index helps you quickly jump to specific data you might be interested in.

Data Organization

Unordered Heap

No organization at all. $O(N)$ reads.

(Secondary) Index

Index structure over unorganized data. $O(\ll N)$ random reads for some queries.

Clustered (Primary) Index

Index structure over clustered data. $O(\ll N)$ sequential reads for some queries.

Hash Indexes

A hash function $h(k)$ is ...

... deterministic

The same $k$ always produces the same hash value.

... (pseudo-)random

Different $k$s are unlikely to have the same hash value.

Modulus $h(k)\%N$ gives you a random number in $[0, N)$

Problems

$N$ is too small

Too many overflow pages (slower reads).

$N$ is too big

Too many normal pages (wasted space).

Idea: Resize the structure as needed

To keep things simple, let's use $$h(k) = k$$

(you wouldn't actually do this in practice)

Problems

Changing hash functions reallocates everything

Only double/halve the size of a hash function

Changing sizes still requires reading everything

Idea: Only redistribute buckets that are too big

Dynamic Hashing

• Add a level of indirection (Directory).
• A data page $i$ can store data with $h(k)%2^n=i$ for any $n$.
• Double the size of the directory (almost free) by duplicating existing entries.
• When bucket $i$ fills up, split on the next power of 2.
• Can also merge buckets/halve the directory size.

CDF-Based Indexing

"The Case for Learned Index Structures"
by Kraska, Beutel, Chi, Dean, Polyzotis

Cumulative Distribution Function (CDF)

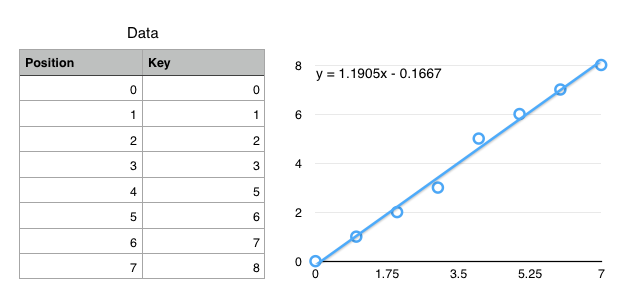
$f(key) \mapsto position$

(not exactly true, but close enough for today)

Using CDFs to find records

Ideal: $f(k) = position$

$f$ encodes the exact location of a record

Ok: $f(k) \approx position$ ($\left|f(k) - position\right| < \epsilon$)

$f$ gets you to within $\epsilon$ of the key

Only need local search on one (or so) leaf pages.

Simplified Use Case: Static data with "infinite" prep time.

How to define $f$?

• Linear ($f(k) = a\cdot k + b$)
• Polynomial ($f(k) = a\cdot k + b \cdot k^2 + \ldots$)
• Neural Network ($f(k) = $)

We have infinite prep time, so fit a (tiny) neural network to the CDF.

Neural Networks

Extremely Generalized Regression
Essentially a really really really complex, fittable function with a lot of parameters.
Captures Nonlinearities
Most regressions can't handle discontinuous functions, which many key spaces have.
No Branching
if statements are really expensive on modern processors.
(Compare to B+Trees with $\log_2 N$ if statements)

Summary

Tree Indexes

$O(\log N)$ access, supports range queries, easy size changes.

Hash Indexes

$O(1)$ access, doesn't change size efficiently, only equality tests.

CDF Indexes

$O(1)$ access, supports range queries, static data only.