Indexes

Today's Focus

$\sigma_C(R)$ and $(\ldots \bowtie_C R)$

(Finding records in a table really fast)

Indexing Strategies

Rearrange the data.

Put things in a predictable location or a specific order.

("clustering" the data)

Wrap the data.

Record where specific data values live

("indexing" the data).

Data Organization

Unordered Heap

No organization at all. $O(N)$ reads.

(Secondary) Index

Index structure over unorganized data. $O(\ll N)$ random reads for some queries.

Clustered (Primary) Index

Index structure over clustered data. $O(\ll N)$ sequential reads for some queries.

Data Organization

Data Organization

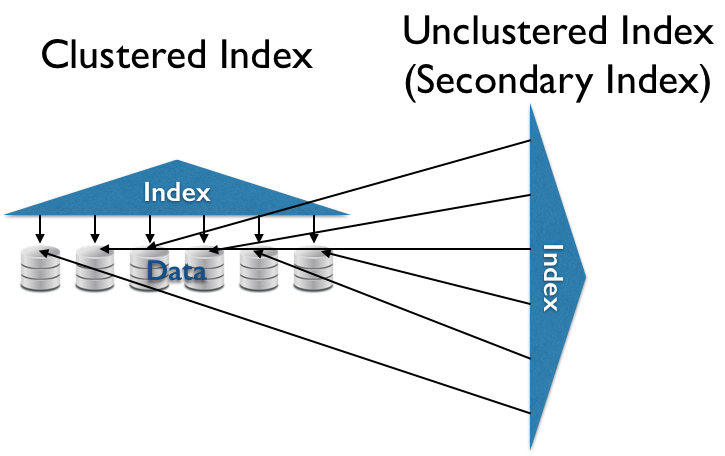
Index Types

Tree-Based

A hierarchy of decisions lead to data at the leaves.

Hash-Based

A hash function puts data in predictable locations.

CDF-Based (new)

A more complex function predicts where data lives.

Tree-Based Indexes

Tree-Based Indexes

Challenges

Balance

Bad question orders lead to poor performance!

IO

Each access to a binary tree node is a random access.

Which Dimension

Why limit ourselves to asking about one dimension?

Worst-Case Tree?

Best-Case Tree?

Binary Trees are Bad for IO

Every step of binary search is a random access

Every tree node access is a random access

Random access IO is bad.

Idea: Load a bunch of binary tree nodes together.

Binary Tree: $1$ separator & $2$ pointers

$log_2(N)$ Deep

$K$-ary Tree: $(K-1)$ separators & $K$ pointers

$log_K(N)$ Deep

Important: You still need to do binary search on each node of a $K$-ary tree, but now you're doing random access on memory (or cache) instead of disk (or memory)

ISAM Trees

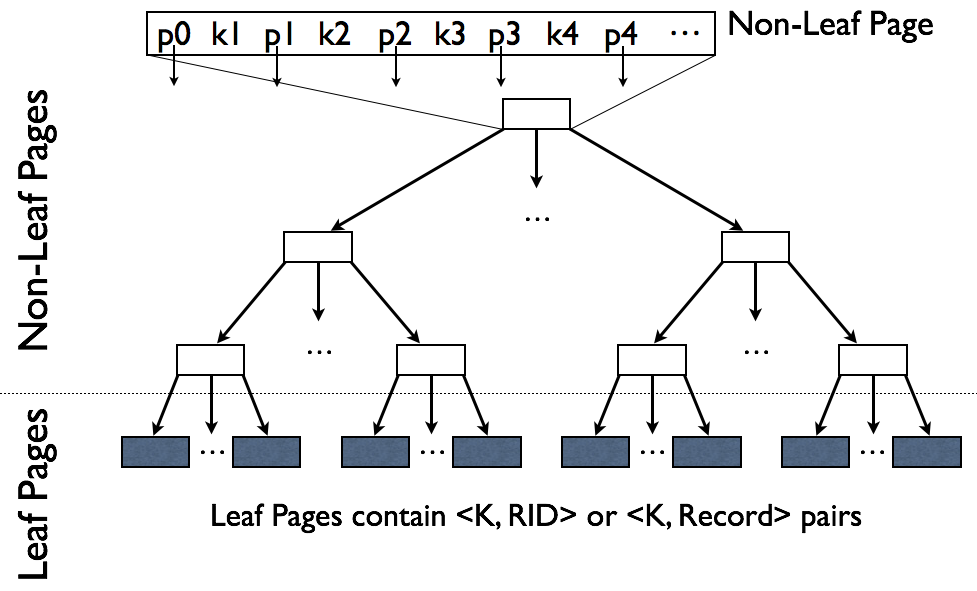
How do you handle updates?

B+Tree = ISAM + Updates

Challenges

• Finding space for new records
• Keeping the tree balanced as new records are added

Idea 1: Reserve space for new records

Just maintaining open space won't work forever...

Rules of B+Trees

Keep space open for insertions in inner/data nodes.

‘Split’ nodes when they’re full

Avoid under-using space

‘Merge’ nodes when they’re under-filled

Maintain Invariant: All Nodes ≥ 50% Full

(Exception: The Root)

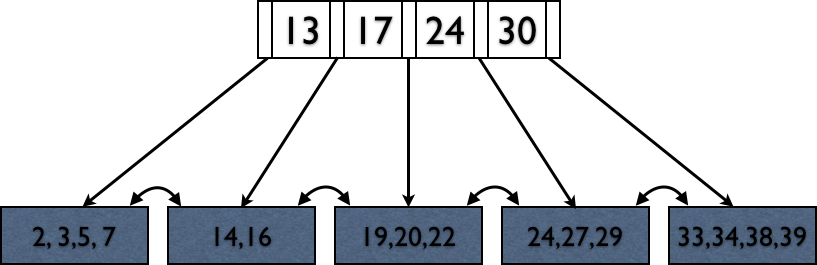
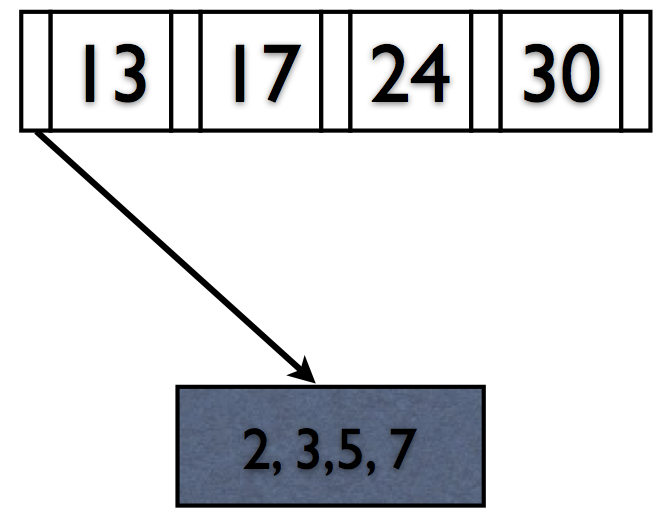
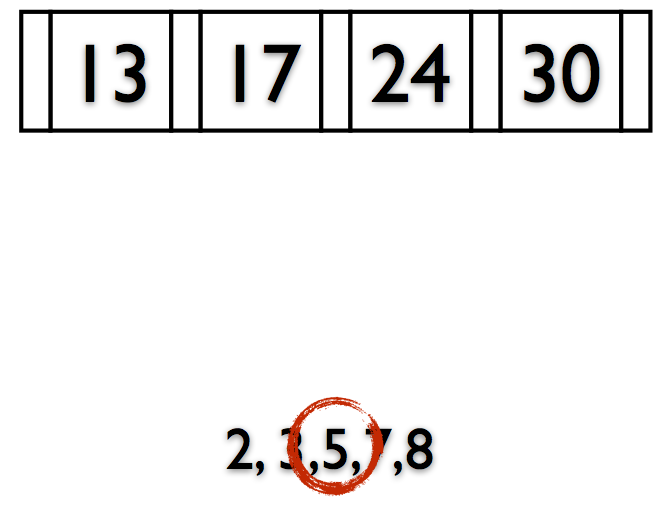
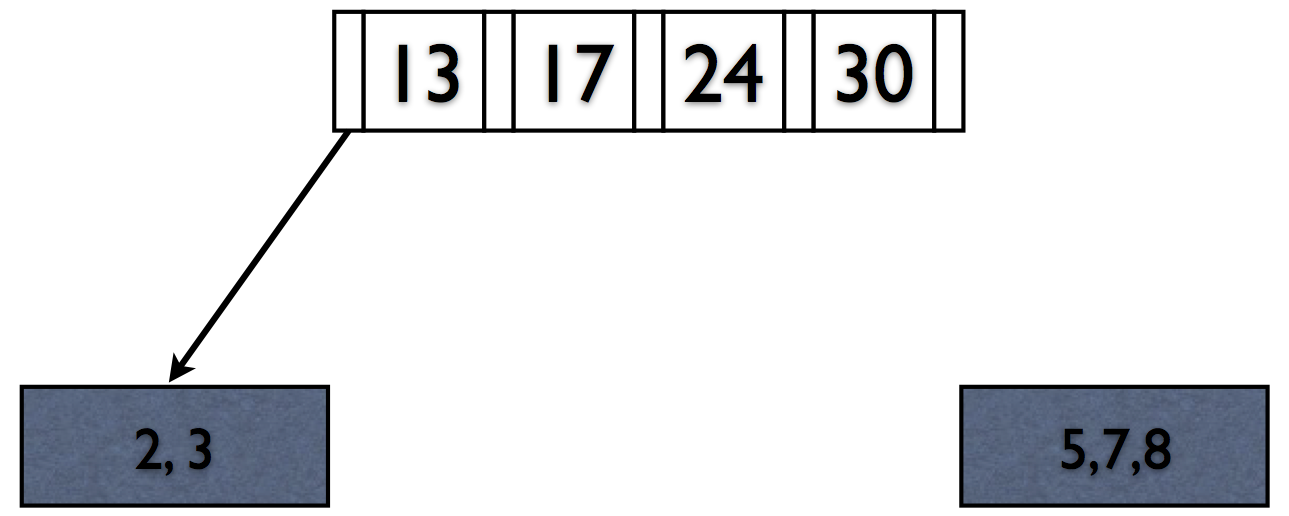
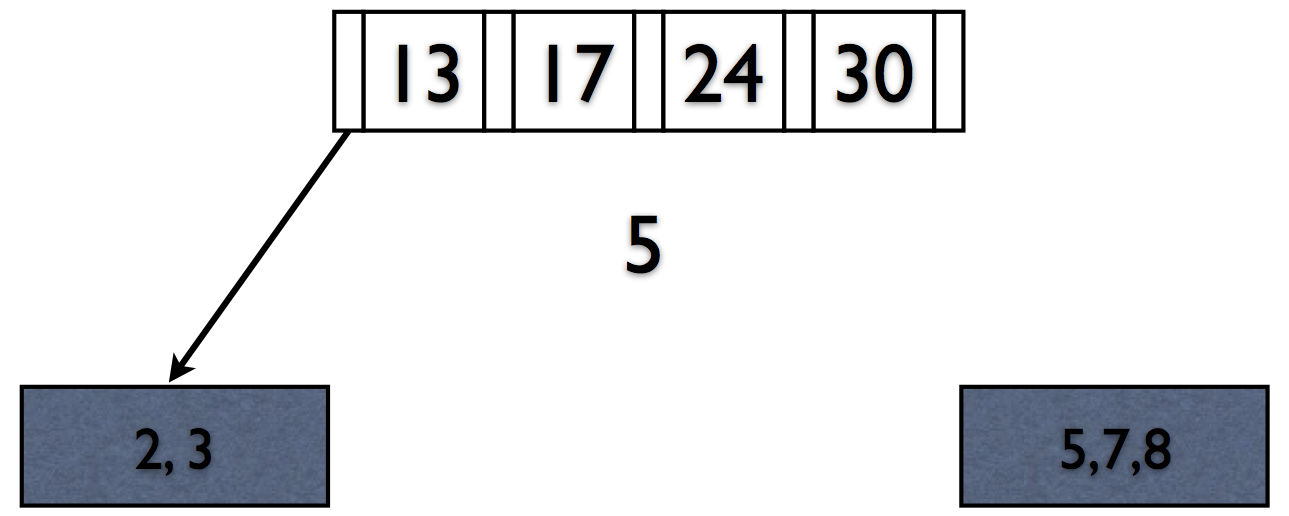
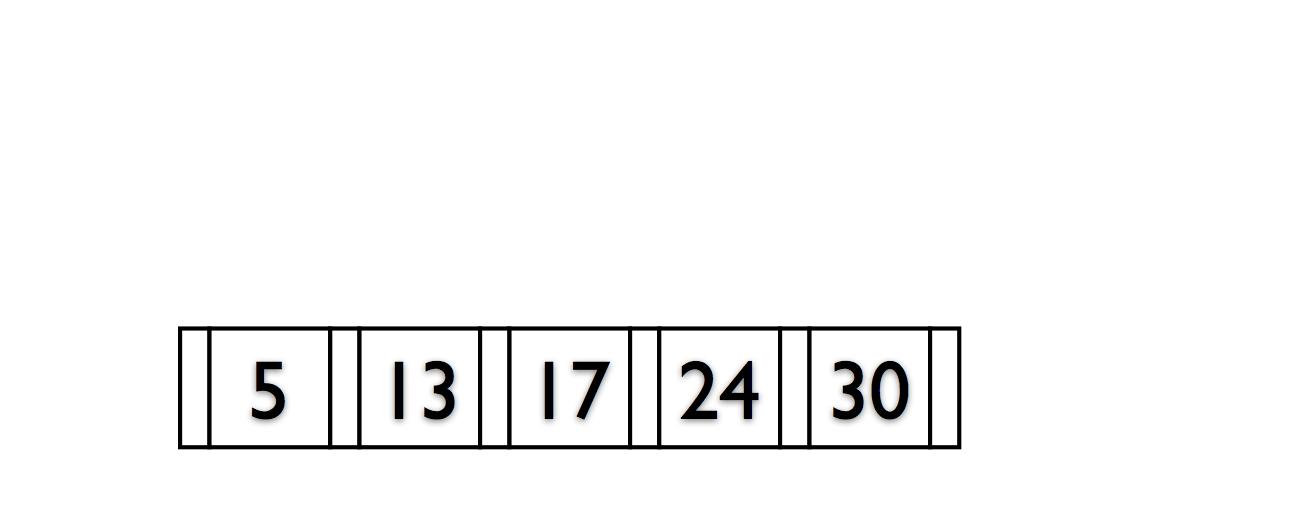
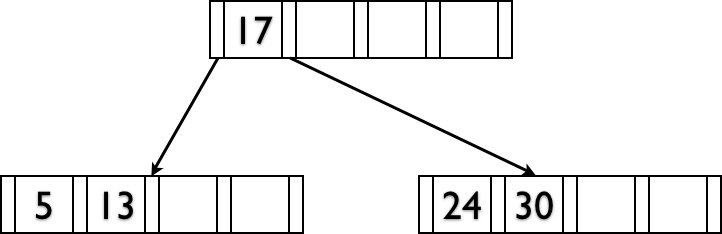
Deletions reverse this process (at 50% fill).